Currently Empty: $0.00
1. Basic Idea
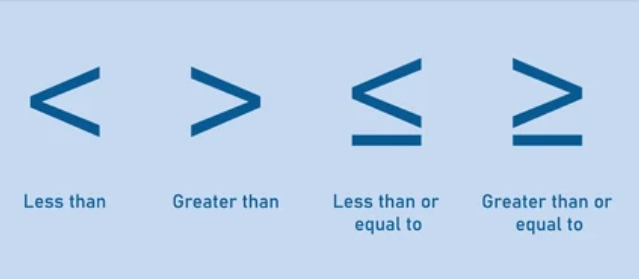
An inequality compares two expressions using symbols:
< → less than
> → greater than
≤ → less than or equal to
≥ → greater than or equal to
Example:
3x+2>113x + 2 > 113x+2>11
🔹 2. Solving Linear Inequalities
Steps:
Simplify both sides (remove parentheses, combine like terms).
Isolate the variable on one side.
Important:
🔸 When you multiply or divide by a negative number, flip the inequality sign.
Example:
−2x+5>9-2x + 5 > 9−2x+5>9
Subtract 5:
−2x>4-2x > 4−2x>4
Divide by -2 (flip sign):
x<−2x < -2x<−2
✅ Final Answer: x<−2x < -2x<−2
🔹 3. Graphing on a Number Line
| Symbol | Circle Type | Shade Direction |
|---|---|---|
| <<< or >>> | Open circle | Left (<) or Right (>) |
| ≤≤≤ or ≥≥≥ | Closed circle | Left (≤) or Right (≥) |
Example:
x≥−2x ≥ -2x≥−2 → Closed circle at -2, shade right
🔹 4. Interval Notation
| Inequality | Interval Notation |
|---|---|
| x>ax > ax>a | (a,∞)(a, ∞)(a,∞) |
| x≥ax ≥ ax≥a | [a,∞)[a, ∞)[a,∞) |
| x<ax < ax<a | (−∞,a)(-∞, a)(−∞,a) |
| x≤ax ≤ ax≤a | (−∞,a](-∞, a](−∞,a] |
🔹 5. Compound Inequalities
Two inequalities combined using “AND” or “OR”.
A. AND Inequalities (Intersection)
The solution satisfies both inequalities.
Think: “Between two values.”
Example:
3<x≤73 < x ≤ 73<x≤7
means xxx is greater than 3 and less than or equal to 7.
Interval Notation: (3,7](3, 7](3,7]
Graph: Shade between 3 and 7.
B. OR Inequalities (Union)
The solution satisfies either inequality.
Think: “Outside values.”
Example:
x<2 or x≥5x < 2 \text{ or } x ≥ 5x<2 or x≥5
means xxx is less than 2 or greater than or equal to 5.
Interval Notation: (−∞,2)∪[5,∞)(-∞, 2) ∪ [5, ∞)(−∞,2)∪[5,∞)
Graph: Shade both sides, not between.
🔹 6. Checking Solutions
Always test a point from each region (especially for OR inequalities).
Plug into the original inequality to confirm.
🔹 7. Absolute Value Inequalities
| Type | Interpretation | Solution |
|---|---|---|
| ( | x | < a ) |
| ( | x | ≤ a ) |
| ( | x | > a ) |
| ( | x | ≥ a ) |
Example:
∣x−4∣<3|x – 4| < 3∣x−4∣<3
→ −3<x−4<3-3 < x – 4 < 3−3<x−4<3
Add 4 → 1<x<71 < x < 71<x<7
✅ Answer: (1,7)(1, 7)(1,7)
🔹 8. Special Cases
∣x∣<−a|x| < -a∣x∣<−a → No solution (absolute value can’t be negative).
∣x∣>−a|x| > -a∣x∣>−a → All real numbers (always true).
🔹 9. Compound Inequalities with Fractions
Always clear fractions first!
Example:
2x−34≤5\frac{2x – 3}{4} ≤ 542x−3≤5
Multiply both sides by 4:
2x−3≤202x – 3 ≤ 202x−3≤20
→ x≤11.5x ≤ 11.5x≤11.5
🔹 10. Graphing Tricks
“AND” → Between two points
“OR” → Outside two points
Check boundary points carefully (open/closed).
🔹 11. Common Mistakes to Avoid
❌ Forgetting to flip sign when dividing by negative.
❌ Mixing up AND/OR.
❌ Using open instead of closed circle incorrectly.
❌ Not testing intervals for correctness.
❌ Leaving answer in inequality when asked for interval notation.
🔹 12. Practice Summary Table
| Type | Example | Solution | Graph Type |
|---|---|---|---|
| Linear | 2x−5≥72x – 5 ≥ 72x−5≥7 | x≥6x ≥ 6x≥6 | Right |
| AND | −3<x≤2-3 < x ≤ 2−3<x≤2 | Between | Between |
| OR | x<−4 or x≥1x < -4 \text{ or } x ≥ 1x<−4 or x≥1 | Outside | Two regions |
| Absolute Value | ( | x + 2 | ≥ 5 ) |
Would you like me to include a 1-page pri
Tags: